A Complete Guide to Linear Regression in Python

In this article we covered linear regression using Python in detail. It includes its meaning along with assumptions related to the linear regression technique. After completing this tutorial you will be able to test these assumptions as well as model development and validation in Python.

Table of Contents

---

Python : Linear Regression

Introduction to Linear Regression

Linear Regression is a supervised statistical technique where we try to estimate the dependent variable with a given set of independent variables. We assume the relationship to be linear and our dependent variable must be continuous in nature.
In the following diagram we can see that as horsepower increases mileage decreases thus we can think to fit linear regression. The red line is the fitted line of regression and the points denote the actual observations.

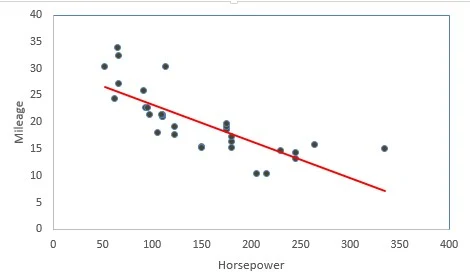
The vertical distance between the points and the fitted line (line of best fit) are called errors. The main idea is to fit this line of regression by minimizing the sum of squares of these errors. This is also known as principle of least squares.

Examples of Linear Regression

• Estimating the price (Y) of a house on the basis of its Area (X1), Number of bedrooms (X2), proximity to market (X3) etc.
• Estimating the mileage of a car (Y) on the basis of its displacement (X1), horsepower(X2), number of cylinders(X3), whether it is automatic or manual (X4) etc.
• To find the treatment cost or to predict the treatment cost on the basis of factors like age, weight, past medical history, or even if there are blood reports, we can use the information from the blood report.

Difference between Simple and Multiple Linear Regression

Simple Linear Regression Model: In this we try to predict the value of dependent variable (Y) with only one regressor or independent variable(X).

Multiple Linear Regression Model: Here we try to predict the value of dependent variable (Y) with more than one regressor or independent variables.

The linear regression model:
Here 'y' is the dependent variable to be estimated, and X are the independent variables and ε is the error term.

Multiple Regression Equation

Assumptions of linear regression

• There must be a linear relationship between the dependent and independent variables.
• Sample observations are independent.
• Error terms are normally distributed with mean 0.
• No multicollinearity - When the independent variables in my model are highly linearly related then such a situation is called multicollinearity.
• Error terms are identically and independently distributed. (Independence means absence of autocorrelation).
• Error terms have constant variance i.e. there is no heteroscedasticity.
• No outliers are present in the data.

Important Model Performance Metrics

Coefficient of Determination (R square)
It suggests the proportion of variation in Y which can be explained with the independent variables. Mathematically, it is the ratio of predicted values and observed values, i.e.

RSquare

If our fit is perfect then

If then R² = 0 indicates a poor fit. Thus it lies between 0 and 1.

If the value of R2 is 0.912 then this suggests that 91.2% of the variation in Y can be explained with the help of given explanatory variables in that model. In other words, it explains the proportion of variation in the dependent variable that is explained by the independent variables.

R square solely not such a good measure:
On addition of a new variable the error is sure to decrease, thus R square always increases whenever a new variable is added to our model. This may not describe the importance of a variable.

For eg. In a model determining the price of the house, suppose we had the variables GDP, Inflation rate, Area. If we add a new variable: no. of plane crashes (which is irrelevant) then still R square will increase.

Adjusted R square:
Adjusted R square is given by: 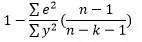or

Adjusted R-Square

where k is the no. of regressors or predictors.
Adjusted R square will always be less than or equal to R square.

On addition of a variable then R square in numerator and 'k' in the denominator will increase. If the variable is actually useful then R square will increase by a large amount and 'k' in the denominator will be increased by 1. Thus the magnitude of increase in R square will compensate for increase in 'k'. On the other hand, if a variable is irrelevant then on its addition R square will not increase much and hence eventually adjusted R square will increase.

Thus as a general thumb rule if adjusted R square increases when a new variable is added to the model, the variable should remain in the model. If the adjusted R square decreases when the new variable is added then the variable should not remain in the model.

Why error terms should be normally distributed?
For parameter estimate (i.e. estimating the β_i’s) we don't need that assumption. But, if it is not a normal distribution, some of those hypotheses tests which we will be doing as part of diagnostics may not be valid.

For example: To check whether the Beta (the regression coefficient) is significant or not, I'll do a T-test. So, if my error is not a normal distribution, then the statistic I derive may not be a T-distribution. So, my diagnostic test or hypotheses test is not valid. Similarly, F-test for linear regression which checks whether any of the independent variables in a multiple linear regression model are significant will be not be viable.

Why is expectation of error always zero?

The error term is the deviation between observed points and the fitted line. The observed points will be above and below the fitted line, so if I took the average of all the deviations, it should be 0 or near 0. Zero conditional mean is there which says that there are both negative and positive errors which cancel out on an average. This helps us to estimate dependent variable precisely.

Why multicollinearity is a problem?

If my Xi’s are highly correlated then |X’X| will be close to 0 and hence inverse of (X’X) will not exist or will be indefinitely large. Mathematically, which will be indefinitely large in presence of multicollinearity. Long story in short, multicollinearity increases the estimate of standard error of regression coefficients which makes some variables statistically insignificant when they should be significant.

How can you detect multicollinearity?

1. Bunch Map Analysis: By plotting scatter plots between various Xi’ s we can have a visual description of how the variables are related.
2. Correlation Method: By calculating the correlation coefficients between the variables we can get to know about the extent of multicollinearity in the data.
3. VIF (Variance Inflation Factor) Method: Firstly we fit a model with all the variables and then calculate the variance inflation factor (VIF) for each variable. VIF measures how much the variance of an estimated regression coefficient increases if your predictors are correlated. The higher the value of VIF for ith regressor, the more it is highly correlated to other variables.
   

What is Variance Inflation Factor?

Variance inflation factor (VIF) for an explanatory variable is given 1/(1-R^2 ) . Here, we take that particular X as response variable and all other explanatory variables as independent variables. So, we run a regression between one of those explanatory variables with remaining explanatory variables.

Detecting heteroscedasticity

1. Graphical Method: Firstly do the regression analysis and then plot the error terms against the predicted values( Yi^). If there is a definite pattern (like linear or quadratic or funnel shaped) obtained from the scatter plot then heteroscedasticity is present.
2. Goldfeld Quandt (GQ)Test: It assumes that heteroscedastic variance σi2 is positively related to one of the explanatory variables And errors are assumed to be normal. Thus if heteroscedasticity is present then the variance would be high for large values of X.

Steps for GQ test:

1. Order/ rank (ascending) the observations according to the value of Xi beginning with the lowest X value.
2. Omit ‘c’ central observations and ide the remaining (n-c) observations into 2 groups of (n-c)/2 observations each.
3. Fit separate OLS regression to both the groups and obtain residual sum of squares (RSS1 and RSS2) for both the groups.
4. Obtain F = RSS2/ RSS1

It follows F with ((n-c)/2-k) d.f. both both numerator and denominator.
Where k is the no. of parameters to be estimated including the intercept.
If errors are homoscedastic then the two variances RSS2 and RSS1 turn out to be equal i. e. F will tend to 1.

About Dataset
We have 1030 observations on 9 variables. We try to estimate the Complete compressive strength(CRS) using:

1. Cement - kg in a m3 mixture
2. Blast Furnace Slag - kg in a m3 mixture
3. Fly Ash - kg in a m3 mixture
4. Water - kg in a m3 mixture
5. Superplasticizer - kg in a m3 mixture
6. Coarse Aggregate - kg in a m3 mixture
7. Fine Aggregate - kg in a m3 mixture
8. Age - Day (1-365)

Dataset - Download Data

Python Code : Linear Regression

Importing libraries

Numpy, pandas and matplotlib.pyplot are imported with aliases np, pd and plt respectively.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Loading the data We load our data using pd.read_csv( )

data = pd.read_csv("Concrete_Data.csv")

Now the data is ided into independent (x) and dependent variables (y)

x = data.iloc[:,0:8]
y = data.iloc[:,8:]

Splitting data into training and test sets

Using sklearn we split 80% of our data into training set and rest in test set. Setting random_state will give the same training and test set everytime on running the code.

from sklearn.cross_validation import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.2,random_state = 100) 

Running linear regression using sklearn

Using sklearn linear regression can be carried out using LinearRegression( ) class. sklearn automatically adds an intercept term to our model.

from sklearn.linear_model import LinearRegression
lm = LinearRegression()
lm = lm.fit(x_train,y_train)   #lm.fit(input,output)

The coefficients are given by:

lm.coef_

array([[ 0.12415357,  0.10366839,  0.093371  , -0.13429401,  0.28804259,
         0.02065756,  0.02563037,  0.11461733]])

To store coefficients in a data frame along with their respective independent variables -

coefficients = pd.concat([pd.DataFrame(x_train.columns),pd.DataFrame(np.transpose(lm.coef_))], axis = 1)

0            Cement  0.124154
1             Blast  0.103668
2           Fly Ash  0.093371
3             Water -0.134294
4  Superplasticizer  0.288043
5                CA  0.020658
6                FA  0.025630
7               Age  0.114617

The intercept is:

lm.intercept_

array([-34.273527])

To predict the values of y on the test set we use lm.predict( )

y_pred = lm.predict(x_test)

Errors are the difference between observed and predicted values.

y_error = y_test - y_pred

R square can be obbtained using sklearn.metrics ( ):

from sklearn.metrics import r2_score
r2_score(y_test,y_pred)

0.62252008774048395

Running linear regression using statsmodels

It is to be noted that statsmodels does not add intercept term automatically thus we need to create an intercept to our model.

import statsmodels.api as sma
X_train = sma.add_constant(x_train) ## let's add an intercept (beta_0) to our model
X_test = sma.add_constant(x_test) 

Linear regression can be run by using sm.OLS:

import statsmodels.formula.api as sm
lm2 = sm.OLS(y_train,X_train).fit()

The summary of our model can be obtained via:

lm2.summary()

"""
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                    CMS   R-squared:                       0.613
Model:                            OLS   Adj. R-squared:                  0.609
Method:                 Least Squares   F-statistic:                     161.0
Date:                Wed, 03 Jan 2018   Prob (F-statistic):          4.37e-162
Time:                        21:29:10   Log-Likelihood:                -3090.4
No. Observations:                 824   AIC:                             6199.
Df Residuals:                     815   BIC:                             6241.
Df Model:                           8                                         
Covariance Type:            nonrobust                                         
====================================================================================
                       coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------------
const              -34.2735     29.931     -1.145      0.253     -93.025      24.478
Cement               0.1242      0.010     13.054      0.000       0.105       0.143
Blast                0.1037      0.011      9.229      0.000       0.082       0.126
Fly Ash              0.0934      0.014      6.687      0.000       0.066       0.121
Water               -0.1343      0.046     -2.947      0.003      -0.224      -0.045
Superplasticizer     0.2880      0.102      2.810      0.005       0.087       0.489
CA                   0.0207      0.011      1.966      0.050    2.79e-05       0.041
FA                   0.0256      0.012      2.131      0.033       0.002       0.049
Age                  0.1146      0.006     19.064      0.000       0.103       0.126
==============================================================================
Omnibus:                        3.757   Durbin-Watson:                   2.033
Prob(Omnibus):                  0.153   Jarque-Bera (JB):                3.762
Skew:                          -0.165   Prob(JB):                        0.152
Kurtosis:                       2.974   Cond. No.                     1.07e+05
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.07e+05. This might indicate that there are
strong multicollinearity or other numerical problems.
"""

The predicted values for test set are given by:

y_pred2 = lm2.predict(X_test) 

Note that both y_pred and y_pred2 are same. It's just these are calculated via different packages.

Calculate R-Squared and Adjusted R-Squared Manually on Test data

We can also calculate r-squared and adjusted r-squared via formula without using any package.

import numpy as np
y_test = pd.to_numeric(y_test.CMS, errors='coerce')
RSS = np.sum((y_pred2 - y_test)**2)
y_mean = np.mean(y_test)
TSS = np.sum((y_test - y_mean)**2)
R2 = 1 - RSS/TSS
R2

n=X_test.shape[0]
p=X_test.shape[1] - 1

adj_rsquared = 1 - (1 - R2) * ((n - 1)/(n-p-1))
adj_rsquared

R-Squared : 0.6225
Adjusted RSquared : 0.60719

Detecting Outliers:
Firstly we try to get the studentized residuals using get_influence( ). The studentized residuals are saved in resid_student.

influence = lm2.get_influence()  
resid_student = influence.resid_studentized_external

Combining the training set and the residuals we have:

   Cement  Blast  Fly Ash  Water  Superplasticizer      CA     FA    Age  \
0   540.0    0.0      0.0  162.0               2.5  1040.0  676.0   28.0   
1   540.0    0.0      0.0  162.0               2.5  1055.0  676.0   28.0   
2   332.5  142.5      0.0  228.0               0.0   932.0  594.0  270.0   
3   332.5  142.5      0.0  228.0               0.0   932.0  594.0  365.0   
4   198.6  132.4      0.0  192.0               0.0   978.4  825.5  360.0   
   Studentized Residuals  
0               1.559672  
1              -0.917354  
2               1.057443  
3               0.637504  
4              -1.170290  

resid = pd.concat([x_train,pd.Series(resid_student,name = "Studentized Residuals")],axis = 1)
resid.head()

If the absolute value of studentized residuals is more than 3 then that observation is considered as an outlier and hence should be removed. We try to create a logical vector for the absolute studentized residuals more than 3

     Cement  Blast  Fly Ash  Water  Superplasticizer     CA     FA  Age  \
649   166.8  250.2      0.0  203.5               0.0  975.6  692.6  3.0   
     Studentized Residuals  
649               3.161183  

resid.loc[np.absolute(resid["Studentized Residuals"]) > 3,:]

The index of the outliers are given by ind:

ind = resid.loc[np.absolute(resid["Studentized Residuals"]) > 3,:].index
ind

 Int64Index([649], dtype='int64')

Dropping Outlier
Using the drop( ) function we remove the outlier from our training sets!

y_train.drop(ind,axis = 0,inplace = True)
x_train.drop(ind,axis = 0,inplace = True)  #Interept column is not there
X_train.drop(ind,axis = 0,inplace = True)  #Intercept column is there

Detecting and Removing Multicollinearity
We use the statsmodels library to calculate VIF

from statsmodels.stats.outliers_influence import variance_inflation_factor
[variance_inflation_factor(x_train.values, j) for j in range(x_train.shape[1])]

[15.477582601956859,
 3.2696650121931814,
 4.1293255012993439,
 82.210084751631086,
 5.21853674386234,
 85.866945489015535,
 71.816336942930675,
 1.6861600968467656]

We create a function to remove the collinear variables. We choose a threshold of 5 which means if VIF is more than 5 for a particular variable then that variable will be removed.

def calculate_vif(x):
    thresh = 5.0
    output = pd.DataFrame()
    k = x.shape[1]
    vif = [variance_inflation_factor(x.values, j) for j in range(x.shape[1])]
    for i in range(1,k):
        print("Iteration no.")
        print(i)
        print(vif)
        a = np.argmax(vif)
        print("Max VIF is for variable no.:")
        print(a)
        if vif[a] <= thresh :
            break
        if i == 1 :          
            output = x.drop(x.columns[a], axis = 1)
            vif = [variance_inflation_factor(output.values, j) for j in range(output.shape[1])]
        elif i > 1 :
            output = output.drop(output.columns[a],axis = 1)
            vif = [variance_inflation_factor(output.values, j) for j in range(output.shape[1])]
    return(output)
train_out = calculate_vif(x_train) 

Now we view the training set

train_out.head()

     Cement  Blast  Fly Ash  Superplasticizer  Age

337   275.1    0.0    121.4               9.9   56
384   516.0    0.0      0.0               8.2   28
805   393.0    0.0      0.0               0.0   90
682   183.9  122.6      0.0               0.0   28
329   246.8    0.0    125.1              12.0    3

Removing the variables from the test set.

x_test.head()
x_test.drop(["Water","CA","FA"],axis = 1,inplace = True)
x_test.head()

     Cement  Blast  Fly Ash  Superplasticizer  Age
173   318.8  212.5      0.0              14.3   91
134   362.6  189.0      0.0              11.6   28
822   322.0    0.0      0.0               0.0   28
264   212.0    0.0    124.8               7.8    3
479   446.0   24.0     79.0              11.6    7

Running linear regression again on our new training set (without multicollinearity)

import statsmodels.api as sma
import statsmodels.formula.api as sm
train_out = sma.add_constant(train_out) ## let's add an intercept (beta_0) to our model
x_test.drop(["Water","CA","FA"],axis = 1,inplace = True)
X_test = sma.add_constant(x_test)
lm2 = sm.OLS(y_train,train_out).fit()
lm2.summary()

"""
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                    CMS   R-squared:                       0.570
Model:                            OLS   Adj. R-squared:                  0.567
Method:                 Least Squares   F-statistic:                     216.3
Date:                Wed, 10 Jan 2018   Prob (F-statistic):          6.88e-147
Time:                        15:14:59   Log-Likelihood:                -3128.8
No. Observations:                 823   AIC:                             6270.
Df Residuals:                     817   BIC:                             6298.
Df Model:                           5                                         
Covariance Type:            nonrobust                                         
====================================================================================
                       coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------------
const              -11.1119      1.915     -5.803      0.000     -14.871      -7.353
Cement               0.1031      0.005     20.941      0.000       0.093       0.113
Blast                0.0721      0.006     12.622      0.000       0.061       0.083
Fly Ash              0.0614      0.009      6.749      0.000       0.044       0.079
Superplasticizer     0.7519      0.077      9.739      0.000       0.600       0.903
Age                  0.1021      0.006     16.582      0.000       0.090       0.114
==============================================================================
Omnibus:                        0.870   Durbin-Watson:                   2.090
Prob(Omnibus):                  0.647   Jarque-Bera (JB):                0.945
Skew:                           0.039   Prob(JB):                        0.623
Kurtosis:                       2.853   Cond. No.                     1.59e+03
==============================================================================

Checking normality of residuals We use Shapiro Wilk test from scipy library to check the normality of residuals.

1. Null Hypothesis: The residuals are normally distributed.
2. Alternative Hypothesis: The residuals are not normally distributed.

from scipy import stats
stats.shapiro(lm2.resid)

(0.9983407258987427, 0.6269884705543518)

Since the pvalue is 0.6269 thus at 5% level of significance we can say that the residuals are normally distributed.

Checking for autocorrelation To ensure the absence of autocorrelation we use Ljungbox test.

1. Null Hypothesis: Autocorrelation is absent.
2. Alternative Hypothesis: Autocorrelation is present.

from statsmodels.stats import diagnostic as diag
diag.acorr_ljungbox(lm2.resid , lags = 1) 

(array([ 1.97177212]), array([ 0.16025989]))

Since p-value is 0.1602 thus we can accept the null hypothesis and can say that autocorrelation is absent.

Checking heteroscedasticity Using Goldfeld Quandt we test for heteroscedasticity.

1. Null Hypothesis: Error terms are homoscedastic
2. Alternative Hypothesis: Error terms are heteroscedastic.

import statsmodels.stats.api as sms
from statsmodels.compat import lzip
name = ['F statistic', 'p-value']
test = sms.het_goldfeldquandt(lm2.resid, lm2.model.exog)
lzip(name, test)

[('F statistic', 0.9903), ('p-value', 0.539)]

The p-value is 0.539 hence we can say that the residuals have constant variance. Hence we can say that all the assumptions of our linear regression model are satisfied.

Related Posts

Learn Python : Top 50 Python Tutorials

Spread the Word!
Share Share Tweet

About Author:

Ekta is a Data Science enthusiast, currently in the final year of her post graduation in statistics from Delhi University. She is passionate about statistics and loves to use analytics to solve complex data problems. She is working an an intern, ListenData.

Let's Get Connected: Facebook | LinkedIn