In this article, we will cover the concept of Weight of Evidence (WOE) and Information Value (IV) and how they can be used to improve your predictive model along with the details of how to compute them using SAS, R and Python.
Logistic regression model is one of the most commonly used statistical technique for solving binary classification problem. It is an acceptable technique in almost all the domains. These two concepts - weight of evidence (WOE) and information value (IV) evolved from the same logistic regression technique. These two terms have been in existence in credit scoring world for more than 4-5 decades. They have been used as a benchmark to screen variables in the credit risk modeling projects such as probability of default. They help to explore data and screen variables. It is also used in marketing analytics project such as customer attrition model, campaign response model etc.
What is Weight of Evidence?
The Weight of Evidence (WOE) tells the predictive power of an independent variable in relation to the dependent variable. Since it evolved from credit scoring world, it is generally described as a measure of the separation of good and bad customers. "Bad Customers" refers to the customers who defaulted on a loan. and "Good Customers" refers to the customers who paid back loan.
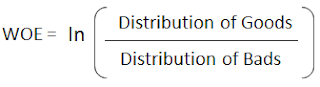 |
| WOE Calculation |
Distribution of Goods - % of Good Customers in a particular group
Distribution of Bads - % of Bad Customers in a particular group
ln - Natural Log
Positive WOE means Distribution of Goods > Distribution of Bads
Negative WOE means Distribution of Goods < Distribution of Bads
Hint : Log of a number > 1 means positive value. If less than 1, it means negative value.
Many people do not understand the terms goods/bads as they are from different background than the credit risk. It's good to understand the concept of WOE in terms of
events and non-events. It is calculated by taking the natural logarithm (log to base e) of division of % of non-events and % of events.
WOE = In(% of non-events ➗ % of events)
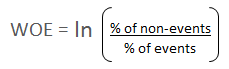 |
| Weight of Evidence Formula |
How to calculate Weight of Evidence?
Follow the steps below to calculate Weight of Evidence
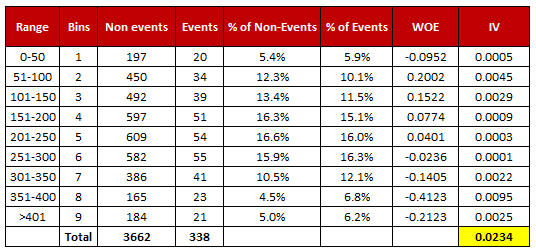
- For a continuous variable, split data into 10 parts (or lesser depending on the distribution).
- Calculate the number of events and non-events in each group (bin)
- Calculate the % of events and % of non-events in each group.
- Calculate WOE by taking natural log of division of % of non-events and % of events
Note : For a categorical variable, you do not need to split the data (Ignore Step 1 and follow the remaining steps)
 |
| Weight of Evidence and Information Value Calculation |
Download :
Excel Template for WOE and IV
Terminologies related to WOE
1. Fine Classing
Create 10/20 bins/groups for a continuous independent variable and then calculates WOE and IV of the variable
2. Coarse Classing
Combine adjacent categories with similar WOE scores
Usage of WOE
Weight of Evidence (WOE) helps to transform a continuous independent variable into a set of groups or bins based on similarity of dependent variable distribution i.e. number of events and non-events.
For continuous independent variables : First, create bins (categories / groups) for a continuous independent variable and then combine categories with similar WOE values and replace categories with WOE values. Use WOE values rather than input values in your model.
data age1;
set age;
if age = . then WOE_age = 0.34615;
if age >= 10 then WOE_age = -0.03012;
if age >= 20 then WOE_age = 0.07689;
run;
proc logistic data=age1 descending;
model y = WOE_age;
run;
For categorical independent variables : Combine categories with similar WOE and then create new categories of an independent variable with continuous WOE values. In other words, use WOE values rather than raw categories in your model. The transformed variable will be a continuous variable with WOE values. It is same as any continuous variable.
Why combine categories with similar WOE?
It is because the categories with similar WOE have almost same proportion of events and non-events. In other words, the behavior of both the categories is same.
Rules related to WOE
- Each category (bin) should have at least 5% of the observations.
- Each category (bin) should be non-zero for both non-events and events.
- The WOE should be distinct for each category. Similar groups should be aggregated.
- The WOE should be monotonic, i.e. either growing or decreasing with the groupings.
- Missing values are binned separately.
Number of Bins (Groups)
In general, 10 or 20 bins are taken. Ideally, each bin should contain at least 5% cases. The number of bins determines the amount of smoothing - the fewer bins, the more smoothing. If someone asks you ' "why not to form 1000 bins?" The answer is the fewer bins capture important patterns in the data, while leaving out noise. Bins with less than 5% cases might not be a true picture of the data distribution and might lead to model instability.
Handle Zero Event/ Non-Event
If a particular bin contains no event or non-event, you can use the formula below to ignore missing WOE. We are adding 0.5 to the number of events and non-events in a group.
AdjustedWOE = ln (((Number of non-events in a group + 0.5) / Number of non-events)) / ((Number of events in a group + 0.5) / Number of events))
How to check correct binning with WOE
1. The WOE should be monotonic i.e. either growing or decreasing with the bins. You can plot WOE values and check linearity on the graph.
2. Perform the WOE transformation after binning. Next, we run logistic regression with 1 independent variable having WOE values. If the slope is not 1 or the intercept is not
ln(% of non-events / % of events) then the binning algorithm is not good.
[Source : Article]
Benefits of Weight of Evidence
Here are some benefits of Weight of Evidence and how it can be used to improve your predictive model.
- It can treat outliers. Suppose you have a continuous variable such as annual salary and extreme values are more than 500 million dollars. These values would be grouped to a class of (let's say 250-500 million dollars). Later, instead of using the raw values, we would be using WOE scores of each classes.
- It can handle missing values as missing values can be binned separately.
- Since WOE Transformation handles categorical variable so there is no need for dummy variables.
- WoE transformation helps you to build strict linear relationship with log odds. Otherwise it is not easy to accomplish linear relationship using other transformation methods such as log, square-root etc. In short, if you would not use WOE transformation, you may have to try out several transformation methods to achieve this.
What is Information Value?
Information value (IV) is one of the most useful technique to select important variables in a predictive model. It helps to rank variables on the basis of their importance. The IV is calculated using the following formula :
IV = ∑ (% of non-events - % of events) * WOE
 |
| Information Value Formula |
Rules related to Information Value
| Information Value |
Variable Predictiveness |
| Less than 0.02 |
Not useful for prediction |
| 0.02 to 0.1 |
Weak predictive Power |
| 0.1 to 0.3 |
Medium predictive Power |
| 0.3 to 0.5 |
Strong predictive Power |
| >0.5 |
Suspicious Predictive Power |
According to Siddiqi (2006), by convention the values of the IV statistic in credit scoring can be interpreted as follows.
If the IV statistic is:
- Less than 0.02, then the predictor is not useful for modeling (separating the Goods from the Bads)
- 0.02 to 0.1, then the predictor has only a weak relationship to the Goods/Bads odds ratio
- 0.1 to 0.3, then the predictor has a medium strength relationship to the Goods/Bads odds ratio
- 0.3 to 0.5, then the predictor has a strong relationship to the Goods/Bads odds ratio.
- > 0.5, suspicious relationship (Check once)
Important Points
- Information value increases as bins / groups increases for an independent variable. Be careful when there are more than 20 bins as some bins may have a very few number of events and non-events.
- Information value is not an optimal feature (variable) selection method when you are building a classification model other than binary logistic regression (for eg. random forest or SVM) as conditional log odds (which we predict in a logistic regression model) is highly related to the calculation of weight of evidence. In other words, it's designed mainly for binary logistic regression model. Also think this way - Random forest can detect non-linear relationship very well so selecting variables via Information Value and using them in random forest model might not produce the most accurate and robust predictive model.
How to calculate WOE and IV for Continuous Dependent Variable
WOE and IV for Continuous Dependent Variable
Python, SAS and R Code : WOE and IV
R Code
Follow the steps below to calculate Weight of Evidence and Information Value in R
Step 1 : Install and Load Package
First you need to install 'Information' package and later you need to load the package in R.
install.packages("Information")
library(Information)
Step 2 : Import your data
#Read Data
mydata <- read.csv("https://stats.idre.ucla.edu/stat/data/binary.csv")
Step 3 : Summarise Data
In this dataset, we have four variables and 400 observations.
The variable admit is a binary target or dependent variable.
summary(mydata)
admit gre gpa rank
Min. :0.000 Min. :220 Min. :2.26 Min. :1.00
1st Qu.:0.000 1st Qu.:520 1st Qu.:3.13 1st Qu.:2.00
Median :0.000 Median :580 Median :3.40 Median :2.00
Mean :0.318 Mean :588 Mean :3.39 Mean :2.48
3rd Qu.:1.000 3rd Qu.:660 3rd Qu.:3.67 3rd Qu.:3.00
Max. :1.000 Max. :800 Max. :4.00 Max. :4.00
Step 4 : Data Preparation
Make sure your independent categorical variables are stored as factor in R. You can do it by using the following method -
mydata$rank <- factor(mydata$rank)
Important Note : The binary dependent variable has to be
numeric before running IV and WOE as per this package. Do not make it factor.
Step 5 : Compute Information Value and WOE
In the first parameter, you need to define your data frame followed by your target variable. In the bins= parameter, you need to specify the number of groups you want to create it for WOE and IV.
IV <- create_infotables(data=mydata, y="admit", bins=10, parallel=FALSE)
It takes all the variables except dependent variable as predictors from a dataset and run IV on them.
This function supports
parallel computing. If you want to run you code in parallel computing mode, you can run the following code.
IV <- create_infotables(data=mydata, y="admit", bins=10, parallel=TRUE)
You can add
ncore= parameter to mention the number of cores to be used for parallel processing.
Information Value in R
In IV list, the list Summary contains IV values of all the independent variables.
IV_Value = data.frame(IV$Summary)
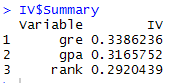 |
| Information Value Scores |
To get WOE table for variable
gre, you need to call Tables list from IV list.
print(IV$Tables$gre, row.names=FALSE)
print(IV$Tables$gre, row.names=FALSE)
gre N Percent WOE IV
[220,420] 38 0.0950 -1.3748 0.128
[440,480] 40 0.1000 -0.0820 0.129
[500,500] 21 0.0525 -1.4860 0.209
[520,540] 51 0.1275 0.2440 0.217
[560,560] 24 0.0600 -0.3333 0.223
[580,600] 52 0.1300 -0.1376 0.225
[620,640] 51 0.1275 0.0721 0.226
[660,660] 24 0.0600 0.7653 0.264
[680,720] 53 0.1325 0.0150 0.265
[740,800] 46 0.1150 0.7653 0.339
To save it in a data frame, you can run the command below-
gre = data.frame(IV$Tables$gre)
Plot WOE Scores
To see trend of WOE variables, you can plot them by using
plot_infotables function.
plot_infotables(IV, "gre")
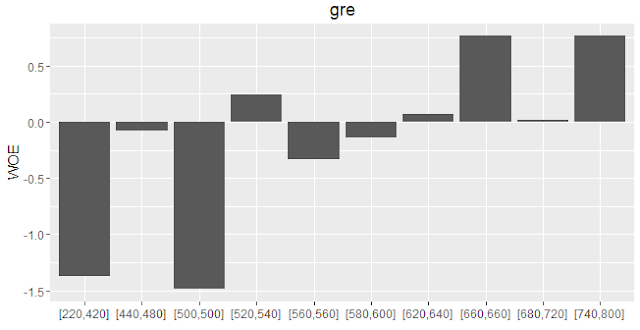 |
| WOE Plot |
To generate multiple charts on one page, you can run the following command -
plot_infotables(IV, IV$Summary$Variable[1:3], same_scale=FALSE)
 |
| MultiPlot WOE |
Important Point
It is important to note here the number of bins for 'rank' variable. Since it is a categorical variable, the number of bins would be according to unique values of the factor variable. The parameter bins=10 does not work for a factor variable.
Python Code
Here are the steps on how to calculate Weight of Evidence and Information Value in Python:
Load Required Python Packages
You can import packages by using import module in Python. The 'as' keyword is used for alias. Instead of using the package name, we can use alias to call any function from the package.
#Load Required Packages
import pandas as pd
import numpy as np
By using
read_csv( ) function, we can read CSV file into Python.
#Read Data
mydata = pd.read_csv("https://stats.idre.ucla.edu/stat/data/binary.csv")
Python Function to calculate Information Value and WOE
def iv_woe(data, target, bins=10, show_woe=False):
#Empty Dataframe
newDF,woeDF = pd.DataFrame(), pd.DataFrame()
#Extract Column Names
cols = data.columns
#Run WOE and IV on all the independent variables
for ivars in cols[~cols.isin([target])]:
if (data[ivars].dtype.kind in 'bifc') and (len(np.unique(data[ivars]))>10):
binned_x = pd.qcut(data[ivars], bins, duplicates='drop')
d0 = pd.DataFrame({'x': binned_x, 'y': data[target]})
else:
d0 = pd.DataFrame({'x': data[ivars], 'y': data[target]})
d0 = d0.astype({"x": str})
d = d0.groupby("x", as_index=False, dropna=False).agg({"y": ["count", "sum"]})
d.columns = ['Cutoff', 'N', 'Events']
d['% of Events'] = np.maximum(d['Events'], 0.5) / d['Events'].sum()
d['Non-Events'] = d['N'] - d['Events']
d['% of Non-Events'] = np.maximum(d['Non-Events'], 0.5) / d['Non-Events'].sum()
d['WoE'] = np.log(d['% of Non-Events']/d['% of Events'])
d['IV'] = d['WoE'] * (d['% of Non-Events']-d['% of Events'])
d.insert(loc=0, column='Variable', value=ivars)
print("Information value of " + ivars + " is " + str(round(d['IV'].sum(),6)))
temp =pd.DataFrame({"Variable" : [ivars], "IV" : [d['IV'].sum()]}, columns = ["Variable", "IV"])
newDF=pd.concat([newDF,temp], axis=0)
woeDF=pd.concat([woeDF,d], axis=0)
#Show WOE Table
if show_woe == True:
print(d)
return newDF, woeDF
In this user-defined function, there are 4 parameters user needs to mention.
data means data frame in which dependent and independent variable(s) are stored.target refers to name of dependent variable.bins refers to number of bins or intervals. By default, it is 10.show_woe = True means you want to print the WOE calculation Table. By default, it is False
How to run Function
It returns two dataframes named iv and woe which contains Information value and WOE of all the variables.
iv, woe = iv_woe(data = mydata, target = 'admit', bins=10, show_woe = True)
print(iv)
print(woe)
Important Points related to Python Script
- Dependent variable specified in target parameter must be binary. 1 refers to event. 0 refers to non-event.
- All numeric variables having no. of unique values less than or equal to 10 are considered as a categorical variable. You can change the cutoff in the code len(np.unique(data[ivars]))>10
- IV score generated from python code won't match with the score derived from R Package as pandas function
qcut( ) does not include lowest value of each bucket. It DOES NOT make any difference in terms of interpretation or decision making based on WOE and IV result.
SAS Code
Here is the SAS program that demonstrates how to calculate the Weight of Evidence and Information Value:
/* IMPORT CSV File from URL */
FILENAME PROBLY TEMP;
PROC HTTP
URL="https://stats.idre.ucla.edu/stat/data/binary.csv"
METHOD="GET"
OUT=PROBLY;
RUN;
OPTIONS VALIDVARNAME=ANY;
PROC IMPORT
FILE=PROBLY
OUT=WORK.MYDATA REPLACE
DBMS=CSV;
RUN;
PROC HPBIN DATA=WORK.MYDATA QUANTILE NUMBIN=10;
INPUT GRE GPA;
ODS OUTPUT MAPPING = BINNING;
RUN;
PROC HPBIN DATA=WORK.MYDATA WOE BINS_META=BINNING;
TARGET ADMIT/LEVEL=BINARY ORDER=DESC;
ODS OUTPUT INFOVALUE = IV WOE = WOE_TABLE;
RUN;
NUMBIN= refers to number of bins you want to create in WOE calculation.INPUT refers to all the continuous independent variablesTARGET Specify target or dependent variable against this statementORDER=DESC tells SAS that 1 refers to event in your target variable
Output values of WOE and IV using above SAS and Python code would match exactly. R package Information implemented slightly different algorithm and cutoff technique so its returned values may differ with the values from Python and SAS code but difference is not huge and interpretation remains same.
Related Tutorials








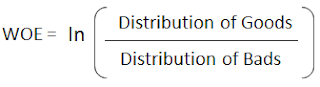
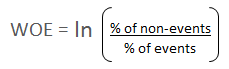





Share Share Tweet